Branching Out into Language
Matilde Marcolli is using the tools of mathematics to dig up the roots and examine the branches of linguistic family trees.
By Whitney Clavin
A history of the words on this page would date back farther than you might think. Modern-day English originated from Germanic and Latin-based languages, which themselves evolved from an even more primitive language known as Proto-Indo- European, whose history stretches possibly as far back as 10,000 years ago when the Neolithic era began.
How do we know this? In the same way that biologists trace the evolution of life with the help of family trees— beginning with single-celled protozoa at the roots and ending with modern-day plants, birds, and other animals at the leaves—linguists use family trees, too, to study the history of languages and map out their common origins.
The Indo-European linguistic family tree is probably the most studied of those; it is a sprawling oak-like collection of several hundred languages, of which English is just one branch. Traditionally, linguists have used historical texts to trace the roots of languages like these, but such texts are not always available, especially when trying to study languages spoken in more remote parts of the world.
So, what are text-less linguists to do? They can turn to a different language—the language of math—and seek the help of the experts who speak it. A number of mathematicians have become interested in linguistics and in mapping out the relationships among languages. They bring to the metaphorical table a number of tools and techniques that allow them to compare cognate, or similar, words among languages and to track changes in the sounds of words, called phonetics. They then use those similarities and changes to tease out the relationships among the languages they are studying.
The challenge with all of these mapping techniques is that, while they work relatively well on the leaves and branches of a language tree, they are often less effective at uncovering the tree’s oldest sections: the roots that are buried most deeply in the past.
Over the past several years, Caltech mathematician Matilde Marcolli, together with her students, has begun developing new computational methods that allow her to build and analyze linguistic trees—and, specifically, to hone in on their oldest sections. To do this, Marcolli is applying several different mathematical methods to the study of language: algebraic geometry, topology, and coding techniques, among others.
“Individually, some of these methods have been applied before,” she says. “But in trying to tackle the structure of syntax in natural languages, you need a broad combination of different mathematical approaches.”
So far, Marcolli’s approach has proved successful. She has shown that algebraic geometry methods can be used to narrow down candidate linguistic trees and identify the ones that best follow evolutionary processes and thus are more likely to be correct. And by applying topological math techniques to these narrowed-down family trees, she has revealed how some of the branches, or subfamilies, have influenced one another through the years. “What I’m most interested in is using mathematical methods to understand how human languages are structured and how the structure has changed over time,” says Marcolli. “By applying different mathematical methods to languages, you can get the methods to talk to each other and provide a more comprehensive look at the tree’s structure.”
Layers of Language
Language, like matter, adheres to a detailed and manylayered structure. At its smallest scale, it is made up of different types of sounds, or phonemes. Different languages have different numbers of phonemes: the East Papuan languages of New Guinea use 11 different distinct phonemes, while the African language family called Khoisan has more than 140 basic sound units, including clicks. At the next level of language structure are words and the varying ways in which words are not only formed but are modified to play different roles in a sentence—such as when the verb “run” changes to the past tense “ran.” This latter process is known as morphology. While English has a moderate degree of morphology, German and Russian have a much higher degree. Vietnamese, on the other hand, generally does not alter its words; thus, this language is considered among the least morphologically complex.
An even higher-scale structure in language is syntax. While morphology is about the way words change, syntax looks at how the meaning of a sentence changes based on the ordering of those words. Syntax differs by language: For instance, many languages put the subject before the verb, as in English, while others, such as the Celtic languages, do the opposite. Another element of syntax has to do with “head directionality,” or the positioning of the main part (or head) of a sentence—the subject and the verb. In head-initial languages such as English, the main part of the sentence comes first, and the rest of the sentence is appended to the end; in head-final languages such as Japanese, the main part of the sentence comes after its complement. For instance, when a Japanese person says, “I want to eat an apple,” they would place the word apple and other words before eat, since eat is considered the head of the sentence.
It is in this area—syntax, or the large-scale structure of language—where the focus of Marcolli’s language research lies. She and other linguistic researchers are looking at variations in the syntax of languages to better understand how they each splintered off from one another and evolved.
“What linguists have already been doing for many decades is trying to classify the way the syntax works in different languages on the basis of what are called binary variables,” says Marcolli, referring to an idea originally introduced by philosopher and linguist Noam Chomsky in the 1960s and 1970s. “You basically ask a yes/no question for all the variables known—for example, does the language put the subject before the verb—and then you compare languages to see how different those variables are.”
Mapping the DNA of Language
To this end, linguists have developed a database of 115 syntax variables for 253 world languages spread across several different language families. The Indo-European languages are well represented in the database, which includes not only English but Spanish, Punjabi, and Persian, to name a few. One way computational linguists use the database is through the “neighborhood-joining method,” in which languages with a greater number of syntax variables in common are placed closer together on the tree.
“These syntax parameters act as a sort of DNA for language. You can apply phylogenetic ideas from biology in order to construct plausible histories of how these languages might have evolved,” says Kevin Shu, a Caltech undergraduate student who worked with Marcolli on her linguistics research. The method is not infallible, of course. If an error finds its way into one of the branches of a family tree, it will propagate deeper and deeper, spreading back to the roots like an infection.
To solve this problem, Marcolli adopted a tool used by mathematical biologists; an algebraic geometry technique developed by UC Berkeley mathematicians Bernd Sturmfels, Lior Pachter (now the Bren Professor of Computational Biology and Computing and Mathematical Sciences at Caltech), and others. Marcolli is the first to apply this tool to linguistic trees to find which are the “healthiest,” or have the fewest errors. The tool looks at the modern-day languages that make up the leaves of the trees and traces backward to the roots to see if the placement of the leaves makes evolutionary and mathematical sense.
“Whatever the modern languages look like now, they are a function of what happened according to some random evolutionary process that has been creating mutations in those languages along the way,” says Marcolli. “The distribution of the binary syntax variables that we observe in language today—those at the leaves of the tree—is produced by that evolutionary process acting on that tree.”
Using their algebraic geometry method, the Caltech researchers were able to narrow in on what is generally accepted as the most accurate of the Indo-European trees, demonstrating that the technique worked in this wellknown language family. Marcolli plans to use the method next on languages that are not as well documented to see if she can better illuminate their murky origins.
One limitation of this geometric method, however, is that it makes a basic assumption that the binary syntactic parameters examined—the subject-verb order and the head directionality, for instance—evolve independently of one another. But, says Marcolli, “there are unknown relationships between the different syntactic parameters that will impact the way languages change and evolve.”
The Shape of Language
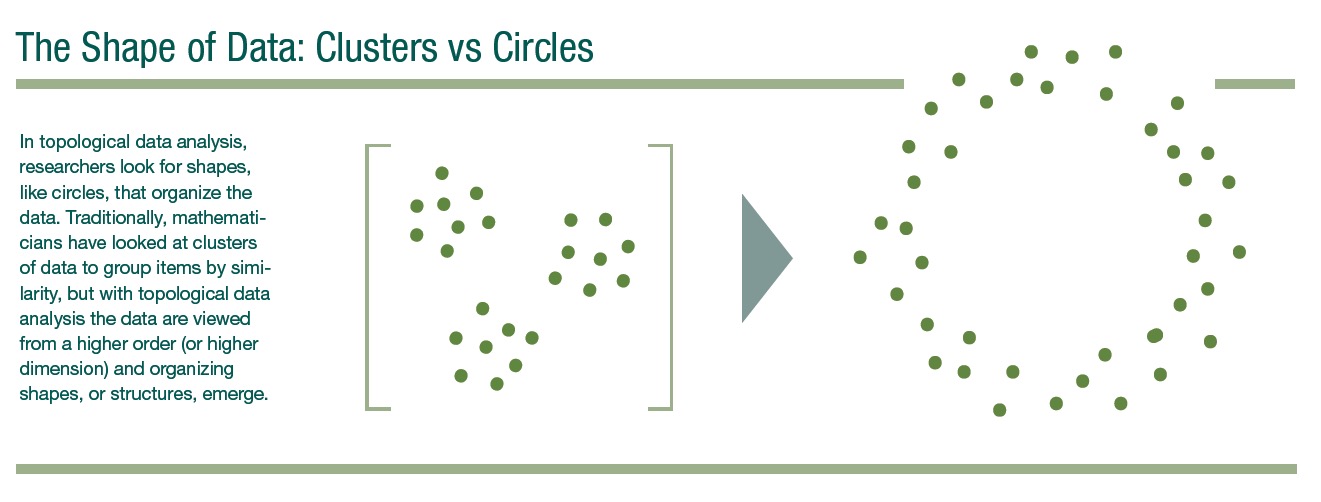
To better understand the interconnectedness of the syntactic variables and to build the most accurate trees, Marcolli and colleagues are taking advantage of a suite of methods to “shape” the linguistic trees in the way an arborist uses a variety of tools to shape an actual tree. These methods include various forms of geometric data analysis and coding theory as well as some novel methods of topological data analysis developed by Stanford mathematician Gunnar Carlsson and others. Topological data analysis is a mathematical technique that allows mathematicians to look at the higher-order structures, or shapes, that organize sets of data. The method, which has been growing in popularity in recent years, can reveal previously unseen connections between data points.
To look for these sorts of obscured connections within the Indo-European language tree, Marcolli and her students applied the topological method to the syntax variables they had already studied using algebraic geometry. They found something unexpected: when one branch of a linguistic family tree influences the growth of another, a loop or circle can show up in the topological data analysis, indicating lateral connections between those languages, as opposed to direct evolutionary pathways. For example, a circle in the data would indicate connections between a tree’s different language branches—branches that had, for the most part, grown independently.
“We found that, in the Indo-European language tree, there is a circle in the data that is mysterious,” says Marcolli. “What it seems to mean is that, at the syntax level, the ancient Greek languages may have influenced other branches of the family tree, such as some of the Slavic languages. This is a phenomenon that linguists have already observed in other ways, but you see it now in the topological data because there’s a circle that comes up. And that means that this is a methodology that will become really useful in the study of linguistic evolution.”
“Languages evolve over time and become separated, but they can come back together again and influence each other,” adds Alexander Port, a Caltech undergraduate student of Marcolli’s who is now doing graduate work at the University of Southern California. Port worked on this project with Marcolli as a part of a computationallinguistics class.
In the future, Marcolli hopes to use studies like these to develop models that describe the structure of languages and all the nuances as well as how groups of people acquire new languages or become bilingual. If scientists can better understand how people learn languages—or “how the ‘syntax calculators’ in our brains work,” as Marcolli puts it—it might lead to new insights into how to create the neural networks needed for artificial intelligence.
But, for now, her focus is on language and its history. As Marcolli demonstrates, the best way to uncover the buried past of words may well be through the use of numbers.